线性映射，是量化交易当中非常重要的一个基础数学知识，频繁用到。那么今天锋哥就带大家学习一下。

 

锋哥的读者朋友，应该普通人占比会更多一些，因此锋哥尽量用通俗的方式来讲，并不会用专业的角度来讲。如果大家需要专业的数学课程，最好是看清华，北大或其他专业学术院校的课程。

 

锋哥只做科普和通俗讲解，大家根据需要，选择继续阅读或者去找专业的课程来看。无论如何，阅读完本文之后，大家应该还是要再去多找一些专业书籍和课程看下，补充和加强理论基础知识。

介绍线性映射

想象一下，你有两根尺子。

第一根尺子（你的大数字尺子）：这根尺子超级超级长！它从 1 开始，一直到 938244343234（这个数超级大，我们叫它“超级大数”吧）。

第二根尺子（你的百分比尺子）：这根尺子短一些，它的刻度从 1% 开始，到 15% 结束。

现在，你想把第一根长尺子上的 任何一个 数字，变成第二根短尺子上对应的 百分比 数字。怎么办呢？

线性映射（就像一条直直的滑梯！）

想象一下，在这两根尺子之间，搭了一条笔直笔直的滑梯：

起点连接：

长尺子的最开头 “1”，正好滑到短尺子的最开头 “1%”。

终点连接：

长尺子的最末尾 “超级大数”，正好滑到短尺子的最末尾 “15%”。

中间点连接：

长尺子正中间的数字是多少呢？就是把“超级大数”差不多切成两半的那个数（比如叫它“中间数”）。这个“中间数”会顺着滑梯滑下来，正好落到短尺子的正中间！短尺子从1%到15%，正中间就是 8%（因为1和15加起来除以2等于8）。

长尺子上在“1”和“中间数”之间的数字，会滑到短尺子上“1%”和“8%”之间的某个位置。

长尺子上在“中间数”和“超级大数”之间的数字，会滑到短尺子上“8%”和“15%”之间的某个位置。

其他点也一样：

长尺子上靠近“1”的数字（比较小的数），会滑到短尺子上靠近“1%”的地方（比较小的百分比）。

长尺子上靠近“超级大数”的数字（很大的数），会滑到短尺子上靠近“15%”的地方（比较大的百分比）。

长尺子上不大不小的数字，就会滑到短尺子上不大不小的百分比位置。

就像均匀排队！

想象长尺子上所有的数字，从1到超级大数，排成一条笔直的长队。

短尺子上所有的百分比，从1%到15%，也排成一条笔直的短队。

线性映射就是让长队里的每一个人，都找到短队里跟他位置相对应的那一个百分比。

队伍最前面的人（1）对应短队最前面的人（1%）。

队伍最后面的人（超级大数）对应短队最后面的人（15%）。

队伍正中间的人（中间数）对应短队正中间的人（8%）。

长队里排在1/4位置的人，就对应短队里排在1/4位置的人（大概是4.5%左右）。

长队里排在3/4位置的人，就对应短队里排在3/4位置的人（大概是11.5%左右）。

总结一下：

线性映射就是一个均匀分配的魔法：

把最小的数字（1）变成最小的百分比（1%）。

把最大的数字（超级大数）变成最大的百分比（15%）。

中间所有的数字，都按照它们在长尺子上离起点和终点的位置比例，均匀地、成比例地变成1%到15%之间对应的百分比。

就像用一根看不见的、笔直的线，把长尺子上的每一个点，都拉到短尺子上一个刚刚好的位置！所以它也叫线性（直的）插值（插进去一个值）。

 

好，上面的讲的比较通俗易懂，接下来，我们继续扩展来讲。

 

数学上的线性映射（linear interpolation）方法，这是一种简单且常用的范围转换技术，确保输入范围均匀地投射到输出范围。

数学公式

线性映射的通用公式为：

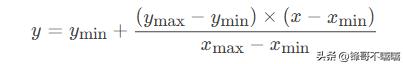
其中：

 

• xx 是输入值（从1到938,244,343,234）。
• yy 是输出值（从1到15，表示百分比值，例如1对应1%，15对应15%）。
• xmin=1xmin=1（输入最小值）。
• xmax=938244343234xmax=938244343234（输入最大值）。
• ymin=1ymin=1（输出最小值）。
• ymax=15ymax=15（输出最大值）。

 

代入具体值：

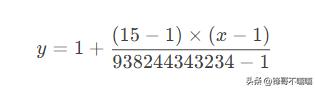
简化后：

 

 

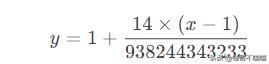
公式说明

• 分母计算：

938244343233。这是一个常数。

• 分子计算：14 x (x - 1) ，其中x−1 表示输入值相对于最小值的偏移量。
• 输出范围：当 x=1 时，y=1（即1%）；当 x=938244343234 时，y=15（即15%）。对于中间值，y 会均匀分布在1到15之间（例如，如果 x 是中间点，y大约是8）。

示例计算

• 示例1：当 x=1（输入最小值）时：

 

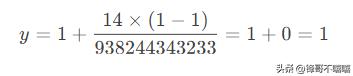
输出 y=1（表示1%）。

• 示例2：当 x=938244343234（输入最大值）时：

 

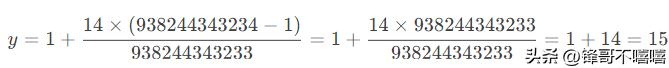
输出 y=15（表示15%）。

• 示例3：当 x=469122171617x=469122171617（近似中点，因为 (1+938244343234)/2≈469122171617.5(1+938244343234)/2≈469122171617.5) 时：

 

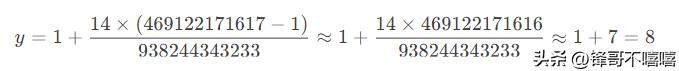
输出 y≈8（表示8%）。实际计算中，由于分母很大，可能需要高精度计算。

算法实现

那么具体在编程中怎么实现呢？以下是用Python写的一个算法的实现

def map_to_percentage(x):
    x_min = 1
    x_max = 938244343234
    y_min = 1.0  # 输出最小值（1%）
    y_max = 15.0  # 输出最大值（15%）
    # 线性映射公式
    y = y_min + (y_max - y_min) * (x - x_min) / (x_max - x_min)
    return y

# 测试
print(map_to_percentage(1))               # 输出: 1.0
print(map_to_percentage(938244343234))    # 输出: 15.0
print(map_to_percentage(469122171617))    # 输出: 约 8.0

在其它编程语言中，实现类似，但注意处理大整数除法时的精度。

具体应用

在量化里面，我们需要把价位差，转换为买入，卖出仓位数量，这个时候，就要进行一系列的操作。比如纳指价位差87点，这个时候买，或者卖，卖多少合适呢？

 

大跌大买，大涨大卖，

小跌小买，小涨小卖。

这个时候，就需要用数学的公式来计算了。